双dq空间的永磁同步电机无位置传感器起动策略
2018-12-24 15:06:22 点击:
基于IF控制的永磁同步电机无位置传感器起动过程中,IF控制与其他观测器类控制策略切换时容易产生电流震荡。针对这一问题,本文提出一种基于双dq空间的永磁同步电机无位置传感器起动策略,分别在虚拟同步坐标系和转子同步坐标系下建立两个dq空间,在两个dq空间下分别建立电机的状态变量和控制变量,将两种控制策略之间的切换转化为两个dq空间的切换。实现了IF控制与其他观测器控制策略的平滑无缝切换。
2
研究背景
本文针对一种可以应用到潜艇、鱼雷、水雷等水下攻击武器或其他水下航行器的无轴泵喷推进器开展研究,研究其无位置传感器复合控制策略。
在永磁同步电机的低速区无位置传感器控制策略中,高频信号注入法的计算和实施比较复杂,对控制器的运算能力要求较高,而且高频信号注入法会产生高频振动噪声,而军用水下航行器对振动噪声要求极为苛刻。
低速区采用IF控制、高速区采用观测器类无位置传感器控制的复合控制策略是一种切实可行的方案。这种复合控制策略的关键是实现低速区控制策略与中高速区控制策略的平滑切换。
3
论文的方法及创新点
传统的切换方法只有一个dq空间,只能以两个坐标系是否重合为切换条件,以谋求这个dq空间的连续性。但是只通过开环的方式设置电流给定,以期望达到两个坐标系重合,没有将两个坐标系之间的误差以反馈的形式引入到切换策略中。
本文所提方法建立了两个dq空间,分别建立电机的状态变量和控制变量,不寻求两个坐标系的重合,而是将两个坐标系的相位差引入到两个dq空间的坐标变换中。由于具有双dq空间,切换条件天然满足,无需特意构造;而且切换过程引入了反馈量,反馈量是两个坐标系的相位差。
IF控制是一种转速开环、电流闭环的控制策略,IF控制不依赖PMSM的转子位置信息。IF控制使用的角度是转速给定积分得到的虚拟转子位置。由虚拟转子位置构建的坐标系称为虚拟同步坐标系,即为dvqv空间,由实际转子位置构建的坐标系称为转子同步坐标系,即为dq空间。电机的状态变量和控制变量在两个dq空间下的表现形式如图1所示。
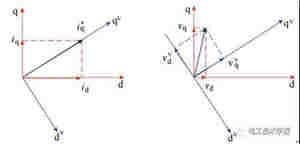
图1 IF控制策略下双dq空间下的(a)状态变量和(b)控制变量
在IF控制策略中使用的是虚拟的dvqv空间,永磁同步电机的电流反馈和电压控制量均是在dvqv空间下表示。当需要进行控制策略切换时,将电机的电流反馈、电流给定和电压控制量同时变换到dq空间。这个坐标变换矩阵是由两个dq空间的相位差决定的,这种变换是顺时完成的。
由于双dq空间对应同样的三相(或者说两相)静止坐标系,双dq空间上的切换动作对静止坐标系不会产生任何影响,从而实现了两种控制策略之间的平滑无缝切换。本文所提起动策略的原理图如图2所示。
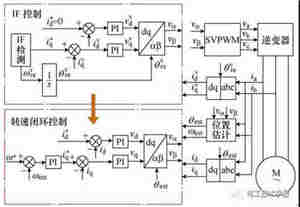
图2 基于双dq空间控制策略切换原理
在实验平台上对本文所提控制策略进行了实验验证,永磁同步电机同轴连接一台直流发电机,直流发电机的电枢绕组连接功率电阻,通过发热的形式将能量释放掉。所使用的电机极对数为15,额定转速为600r/min。
图4和图5给出了控制策略平滑无缝切换的实验波形,图中分别给出了三相电流实验波形、电流环使用的同步坐标系下电流反馈量的实验波形、控制器使用的同步坐标系下电压控制信号的实验波形。从变频器起动运行开始,第5s进行控制策略的切换。
从图4和图5可以看出,由IF控制向基于磁链估计法的无位置传感器控制切换的瞬间,三相电流波形几乎没有任何波动,实现了真正意义上的“无缝”切换。实验结果对基于双dq空间无位置传感器起动策略进行了充分验证。
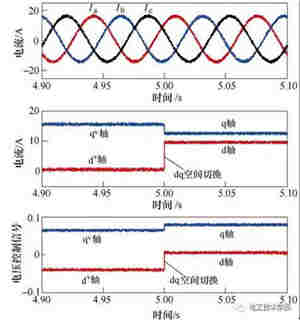
图5 重载实验工况下进行控制策略的切换
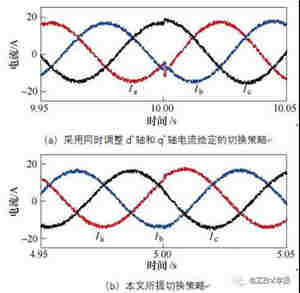
图6给出了两种无位置传感器起动切换策略的效果对比实验波形。在控制策略切换前0.5s,将负载转矩由18N∙m突变至23N∙m,对比两种切换策略的效果。
图6a是采用同时调整dv轴和qv轴电流给定的切换策略,该切换策略需要一定的准备调整时间,因此是在第10s进行控制策略的切换。图6b采用本文所提切换策略,其是在第5s进行控制策略的切换。可以发现由于负载转矩变化,同时调整dv轴和qv轴电流给定的切换策略无法使两个坐标系完全重合,导致切换瞬间三相电流的短时振荡。而本文所提切换策略,则对负载转矩变化不敏感,有更强的适应能力。
4
结论
在虚拟同步坐标系和转子同步坐标系下分别建立了两个dq空间。在两个dq空间上分别建立了电机的状态变量和控制变量。两个dq空间下的变量可以通过变换矩阵进行灵活变换。该变换矩阵和两个dq空间的相位差有关。
通过建立双dq空间,无需像传统控制策略那样尽力使虚拟同步坐标系和转子同步坐标系重合。将控制策略的切换转化为两个dq空间的切换,实现了真正意义上的无缝切换。
2
研究背景
本文针对一种可以应用到潜艇、鱼雷、水雷等水下攻击武器或其他水下航行器的无轴泵喷推进器开展研究,研究其无位置传感器复合控制策略。
在永磁同步电机的低速区无位置传感器控制策略中,高频信号注入法的计算和实施比较复杂,对控制器的运算能力要求较高,而且高频信号注入法会产生高频振动噪声,而军用水下航行器对振动噪声要求极为苛刻。
低速区采用IF控制、高速区采用观测器类无位置传感器控制的复合控制策略是一种切实可行的方案。这种复合控制策略的关键是实现低速区控制策略与中高速区控制策略的平滑切换。
3
论文的方法及创新点
传统的切换方法只有一个dq空间,只能以两个坐标系是否重合为切换条件,以谋求这个dq空间的连续性。但是只通过开环的方式设置电流给定,以期望达到两个坐标系重合,没有将两个坐标系之间的误差以反馈的形式引入到切换策略中。
本文所提方法建立了两个dq空间,分别建立电机的状态变量和控制变量,不寻求两个坐标系的重合,而是将两个坐标系的相位差引入到两个dq空间的坐标变换中。由于具有双dq空间,切换条件天然满足,无需特意构造;而且切换过程引入了反馈量,反馈量是两个坐标系的相位差。
IF控制是一种转速开环、电流闭环的控制策略,IF控制不依赖PMSM的转子位置信息。IF控制使用的角度是转速给定积分得到的虚拟转子位置。由虚拟转子位置构建的坐标系称为虚拟同步坐标系,即为dvqv空间,由实际转子位置构建的坐标系称为转子同步坐标系,即为dq空间。电机的状态变量和控制变量在两个dq空间下的表现形式如图1所示。

图1 IF控制策略下双dq空间下的(a)状态变量和(b)控制变量
在IF控制策略中使用的是虚拟的dvqv空间,永磁同步电机的电流反馈和电压控制量均是在dvqv空间下表示。当需要进行控制策略切换时,将电机的电流反馈、电流给定和电压控制量同时变换到dq空间。这个坐标变换矩阵是由两个dq空间的相位差决定的,这种变换是顺时完成的。
由于双dq空间对应同样的三相(或者说两相)静止坐标系,双dq空间上的切换动作对静止坐标系不会产生任何影响,从而实现了两种控制策略之间的平滑无缝切换。本文所提起动策略的原理图如图2所示。

图2 基于双dq空间控制策略切换原理
在实验平台上对本文所提控制策略进行了实验验证,永磁同步电机同轴连接一台直流发电机,直流发电机的电枢绕组连接功率电阻,通过发热的形式将能量释放掉。所使用的电机极对数为15,额定转速为600r/min。

图4和图5给出了控制策略平滑无缝切换的实验波形,图中分别给出了三相电流实验波形、电流环使用的同步坐标系下电流反馈量的实验波形、控制器使用的同步坐标系下电压控制信号的实验波形。从变频器起动运行开始,第5s进行控制策略的切换。
从图4和图5可以看出,由IF控制向基于磁链估计法的无位置传感器控制切换的瞬间,三相电流波形几乎没有任何波动,实现了真正意义上的“无缝”切换。实验结果对基于双dq空间无位置传感器起动策略进行了充分验证。


图5 重载实验工况下进行控制策略的切换
图6给出了两种无位置传感器起动切换策略的效果对比实验波形。在控制策略切换前0.5s,将负载转矩由18N∙m突变至23N∙m,对比两种切换策略的效果。
图6a是采用同时调整dv轴和qv轴电流给定的切换策略,该切换策略需要一定的准备调整时间,因此是在第10s进行控制策略的切换。图6b采用本文所提切换策略,其是在第5s进行控制策略的切换。可以发现由于负载转矩变化,同时调整dv轴和qv轴电流给定的切换策略无法使两个坐标系完全重合,导致切换瞬间三相电流的短时振荡。而本文所提切换策略,则对负载转矩变化不敏感,有更强的适应能力。
4
结论
在虚拟同步坐标系和转子同步坐标系下分别建立了两个dq空间。在两个dq空间上分别建立了电机的状态变量和控制变量。两个dq空间下的变量可以通过变换矩阵进行灵活变换。该变换矩阵和两个dq空间的相位差有关。
通过建立双dq空间,无需像传统控制策略那样尽力使虚拟同步坐标系和转子同步坐标系重合。将控制策略的切换转化为两个dq空间的切换,实现了真正意义上的无缝切换。
- 上一篇:高压断路器分合闸线圈烧毁原因浅析 2019/1/4
- 下一篇:基于载波重构的级联电力逆变电源功率均衡调制策略 2018/12/24

